O Coronavirus
An analysis of a disease causing global panic.
Lately, the Coronavirus has been prevalent throughout social media and various news outlets. The virus itself, as it is something that society is facing first hand, has interested me and has led me to perform some analysis on its growth and effect in 2020. I’d like to give thanks to Johns Hopkins University for accumulating research on the spread of Coronavirus and providing me with a well-prepared dataset.
Deaths
Summary
As of Februrary 3rd, there was a total of 426 known deaths from Coronavirus. As visualized in the pie chart below, most of the deaths are concentrated in Mainland China. I expected this to be the case as the virus originated from the Chinese city of Wuhan.
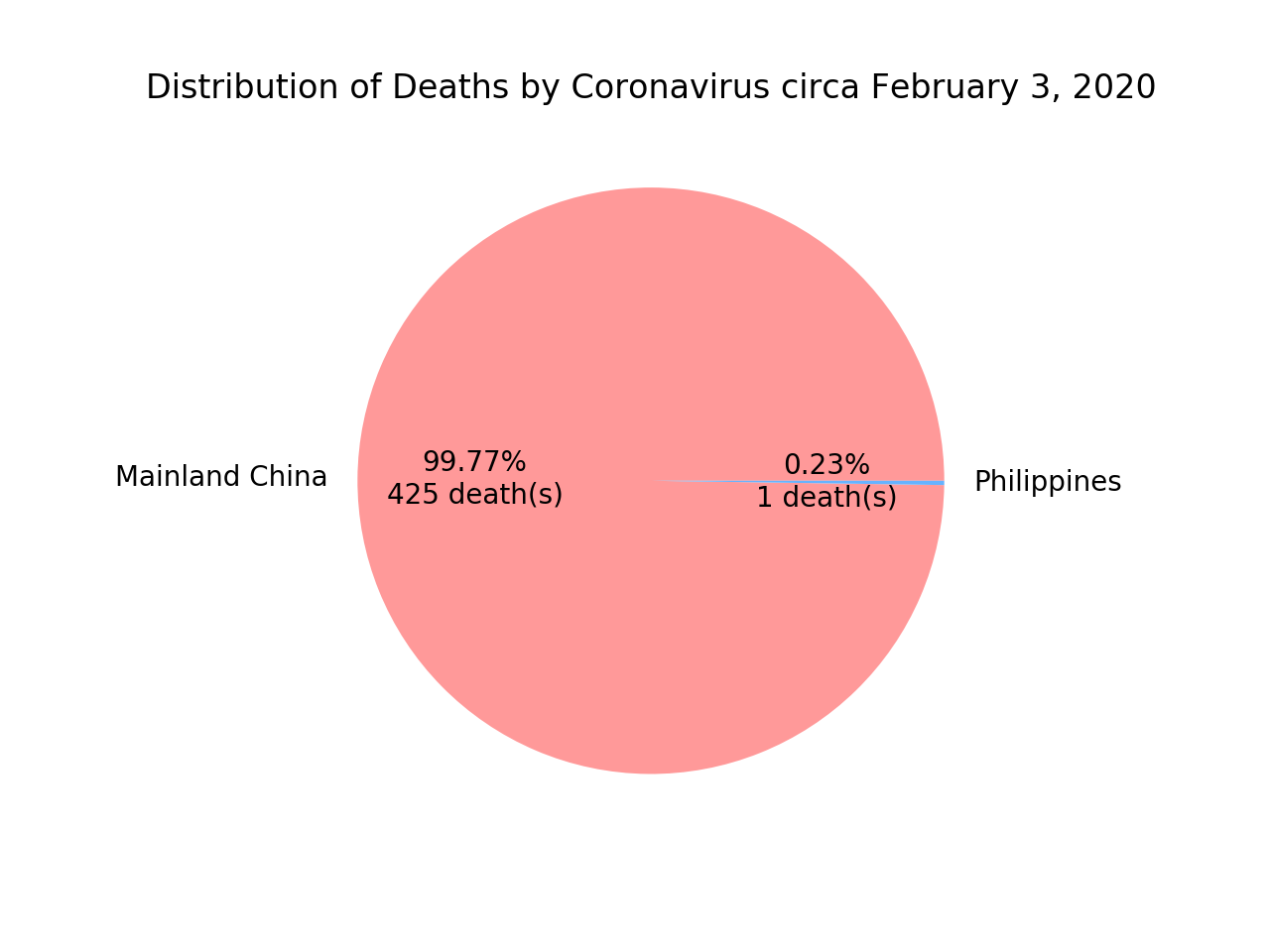
Mainland China
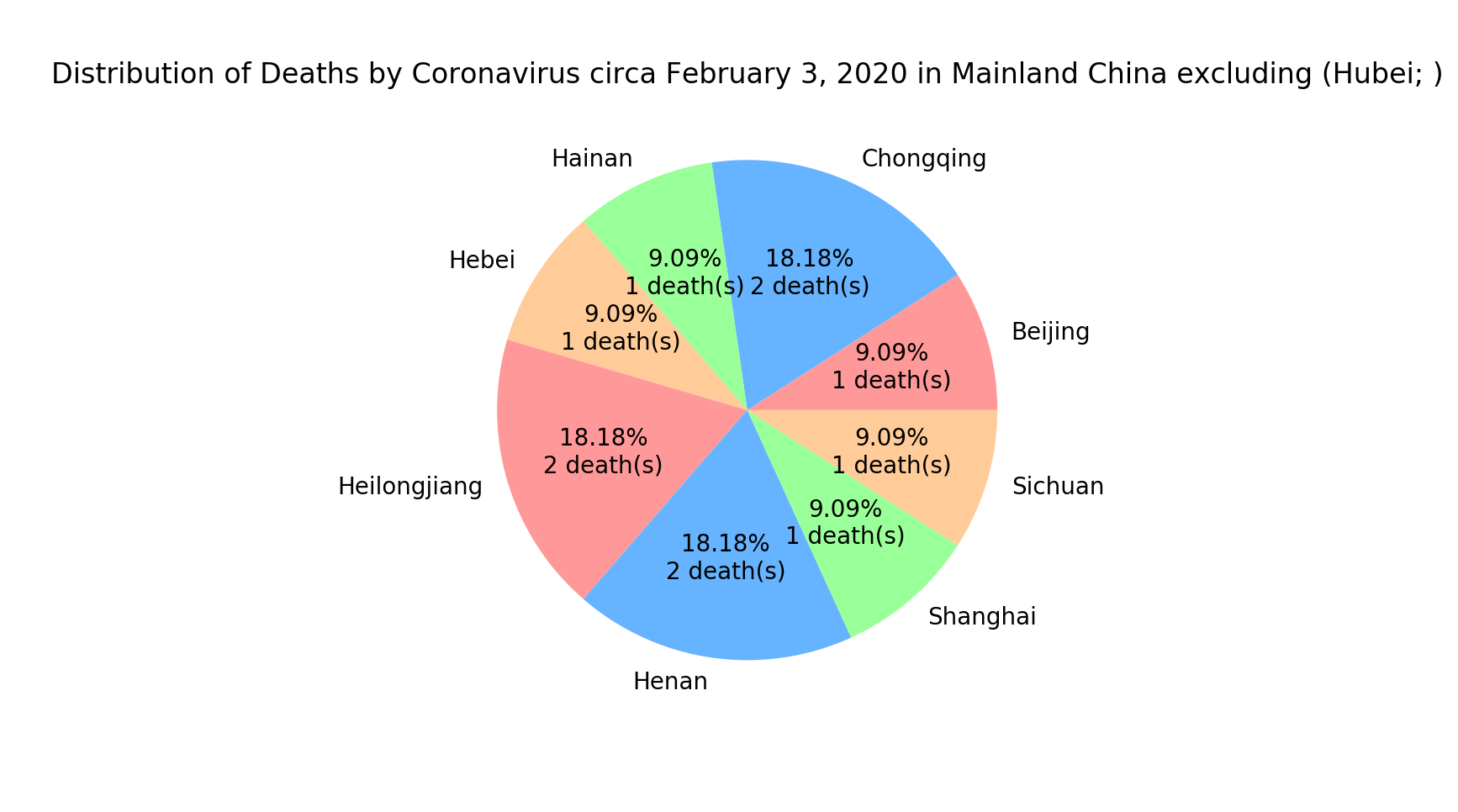
A closer examination of the deaths within Mainland China reveals that the province with the most deaths is Hubei, the province containing Wuhan. One can also acknowledge that several other provinces/states within China have had corresponding deaths. However, it is illustrated that in comparison to Hubei, they have a vastly small number of deaths.
Again, this is expected due to the fact that it is the source of Coronavirus. Furthermore, I suspect that the reason that Hubei’s large number of deaths is due to Hubei’s lockdown (Jan. 23, 2020), in which the province of Hubei shut down several modes of transport in and out of the city to prevent further spread of the disease. These efforts to quarantine the Coronavirus are relatively successful in the sense that only a few deaths were caused outside of Hubei.

Mainland China (Excluding Hubei)
A zoom-in of the sliver in the previous graph demonstrates that there are only 11 other deaths within Mainland China. Furthermore, there are only 1-2 deaths in such geographic areas. In contrast to the common-cold however, this number is non-trivial.
Cases
Although analysis of the deaths from a contagious virus is important, it is impossible to gauge its levels of contagiousness without inspecting its number of cases. By February 3rd, there was a total of 21159 known cases of the Novel Coronavirus. The distribution, similar to the cases is very imbalanced. There is a far greater number of cases in Mainland China / China as opposed to the rest of the world. An important factor to note is that the number of cases in Mainland China itself is 20399, an astonishingly large number of cases. From this statistic alone, one with know knowledge of the disease can infer that the novel Coronavirus is an extremely contagious virus.

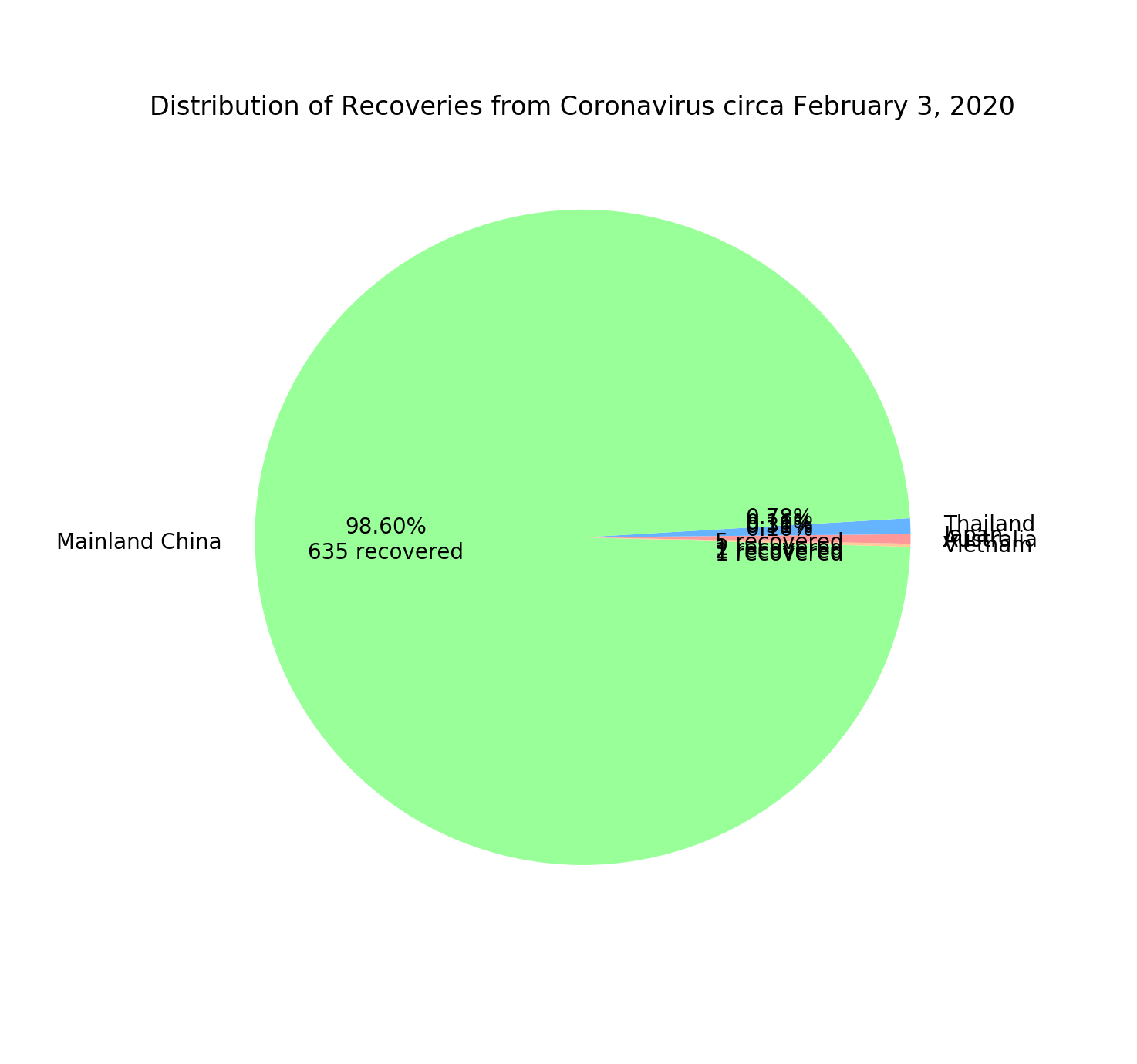
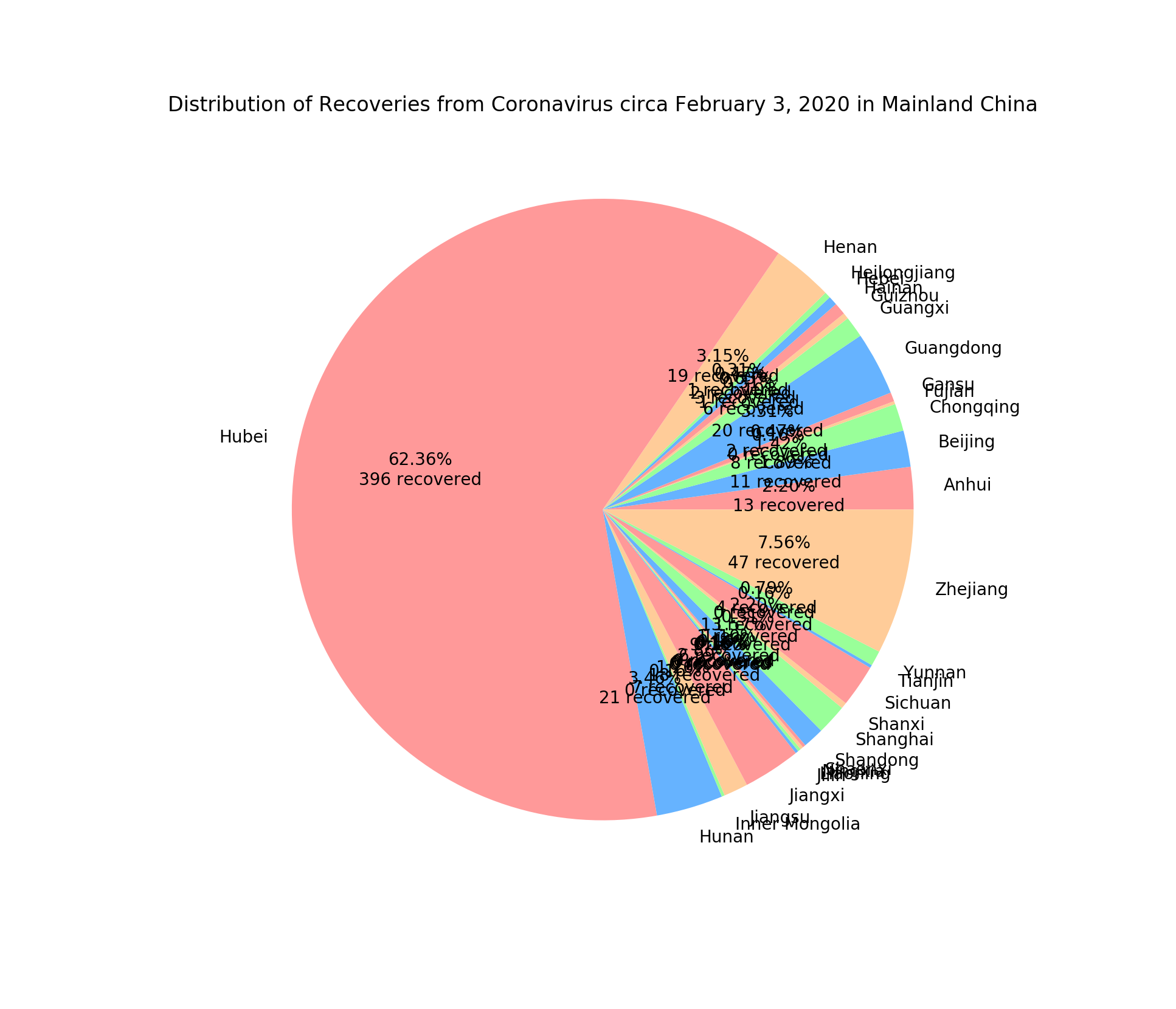
Recoveries
Similar to the number of cases and deaths of Coronavirus, a majority of recoveries of the disease are from Hubei. I assume this to be the case only because Hubei had far more cases to begin with in the first place. More analysis on the metric recovered / number of cases will have to be performed for definitive knowledge.
Growth of Coronavirus
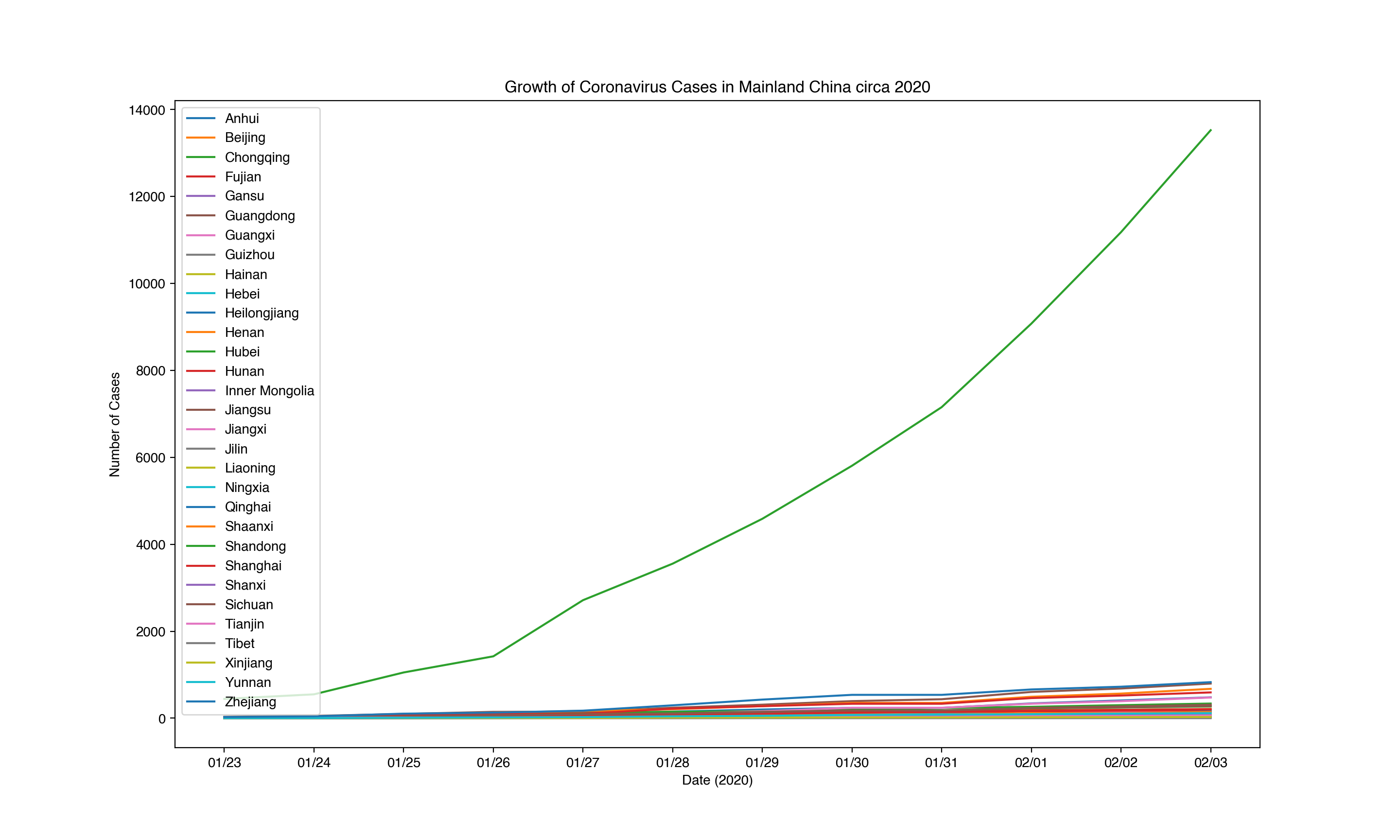
Judging from the previous metrics that have been examined, Mainland China is of the most interest in terms of growth analysis. We observe that of the states and provinces of Mainland China, Hubei’s number of cases demonstrates exponential growth. The other provinces and states also show this property, however, to a smaller degree and with a much smaller growth rate. It makes sense for the spread of the Coronavirus to be modelled by exponential growth because the chances of infection increase per the number of people infected. For example, if one person infects 3 people, and each of those 3 people infects 3 other people, then the number of people infected can be modelled by y = 3^x (exponential growth).
The reason for the growth rate disparity between Hubei and the other provinces and states could in part be explained by Hubei’s lockdown. By restricting travel in and out of Hubei, it makes sense that there would be less cases of Coronavirus outside and in consequence, less spreading of it elsewhere.
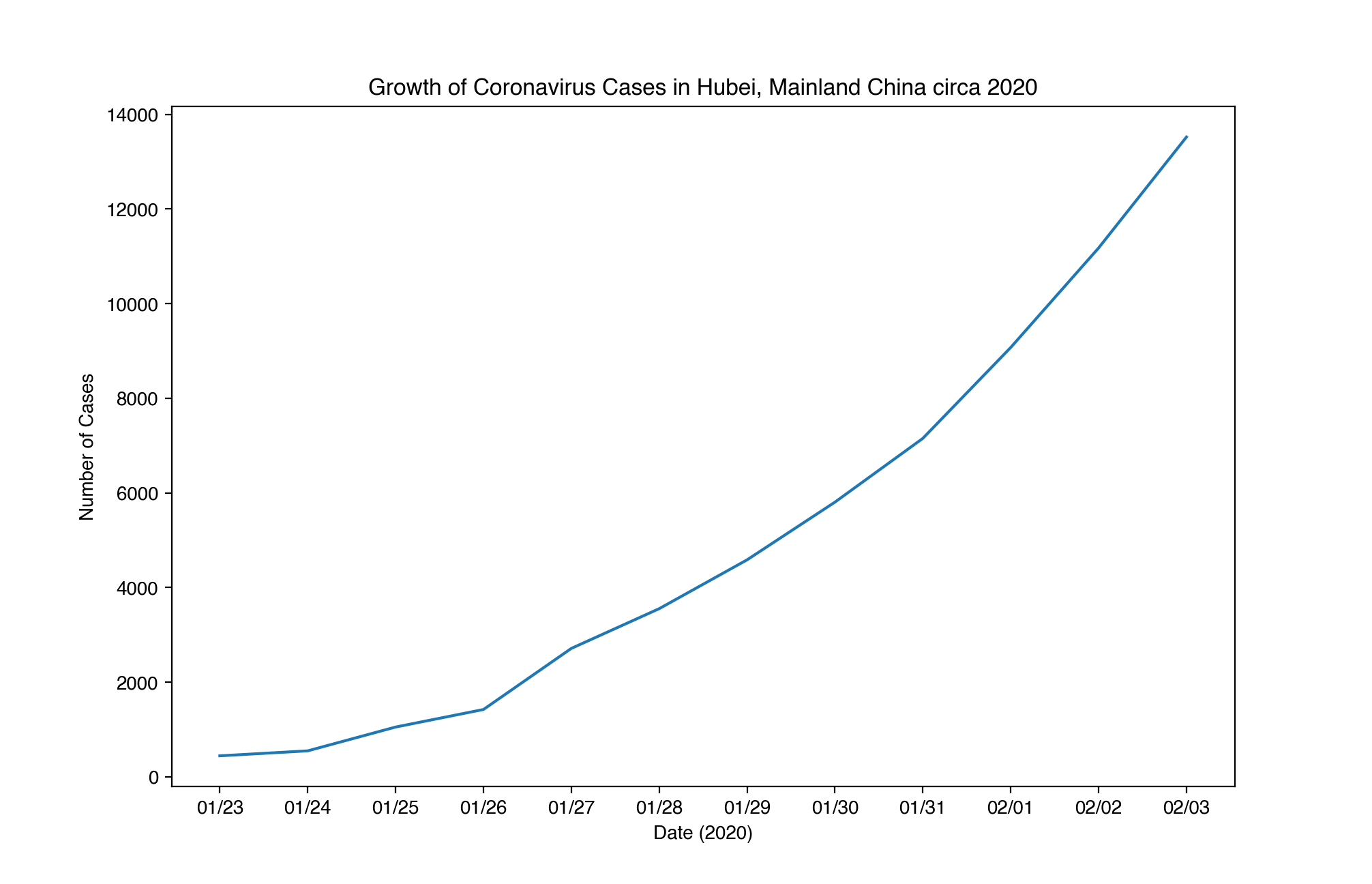
Modelling Growth Data
To really get a solid understanding of the growth of Coronavirus, it’s imperative that we analyze it within a closed system, in which components cannot move in and out freely. Hubei is a perfect example of a system that qualifies this attribute.
If one were to be able to model the growth of the virus, one would be able to make future predictions regarding the epidemic. Let us attempt to model the Coronavirus’ exponential growth using the technique of linear regression. We know for a fact that the exponential growth equation is:
f(x) = a*e^(r*x)
Keep in mind that we have access to the data values f(x) and x, which are the number of Coronavirus cases and number of units of time respectively. It is much more difficult to determine parameters a and r without using a linear approach. Thus, I have converted the equation to the following, which preserves its meaning:
ln(f(x)) = ln(a*e^(r*x))
ln(f(x)) = ln(a) + ln(e^(r*x))
ln(f(x)) = ln(a) + r*x
We now observe that it is possible to model this data using a linear model, where we solve for the parameters ln(a) and r instead of a and r. ln(a) is the y-intercept of the linear function we attempt to predict while r is its slope. Now, I logarithmically scale the values of f(x) such that I have a list of y-values. I then use the linear regression function I have developed to compute the values for ln(a) and r, which happen to be 6.3437 and 0.3121273612433667. This means that the value of a is 568.8760112453323. Thus, the growth of Coronavirus cases in the Hubei Province can be modelled by the equation:
f(x) = (568.876)*e^(0.312*x)
We examine these values and note that the initial number of cases is around 569, on January 23rd. We also note that the growth constant is approximately 0.312. Using this information, we can then model the potential number of cases on a given date in the future.
Conclusion
I do believe that although its growth can be modelled exponentially, the number of cases of Coronavirus will slowly die down. Given that there are many efforts on a global scale to reduce the spreading of the disease and that many individuals are putting more efforts into washing their hands for longer as well as using hand sanitizer often (at least at the University of Waterloo), I’d say that f(x), where f is the number of cases of the virus, will eventually plateau and resemble a sigmoid curve in the future.
